PULSE

By jwxie | | 2 minutes

PULSE: Self-Supervised Photo Upsampling via Latent Space Exploration of Generative Models

🔗 PDF Link 🍺 Github Code
人种变换器?? 😄

Section 1 介绍

效果图（很8错啊~）：

贡献：

  1. 提出了一个新的图像超分辨率范例。传统的方法是使用“重建”的方式来解决超分这个病态的问题，但实际上，这些方法都是通过平均化可能的答案（solution）来实现的，这就不可避免的造成了我们不想见到的模糊。
    核心的一个逻辑应该是：SR出来的图像在经过下采样之后应该与输入的LR图像逼近！
  2. 提出了一个新的方法来解决超分辨率任务。采用了StyleGAN，同时结合无监督训练的方式，从潜在空间（latent space）中去寻找的一个区域，通过这个区域可以实现双向（LR->realistic image->downscaled SR image）变换。
  3. 在高维高斯先验的基础上采用一个传统的方法来对潜在空间进行探索。在PULSE和其他的一些工作中，目的都是在于从潜在空间中找到一个映射，从而讲LR的内容映射到HR，这个映射集应该是从训练集中得到的。正常来说，我们使用对数自然函数来约束我们的模型训练，但是，对数似然函数趋向于去从原点附近寻找这个特征向量（或者说映射）。但是，我们知道，高维高斯分布的高密度区域应该是落在超球面的表面。
    解释一下就是说，LR->HR是一个病态的问题，解必定不是唯一的，同时这种映射也不是一对一的关系，而是一对多，这就必然要求这个映射必须是一个稠密的，而高维高斯分布的高密度区域一般都在超球的表面，那么从原点开始寻找解就是不太合理的一个方法

Section 2 相关工作

在历史上两个重大方案一个是残差学习，一个是亚像素卷积。当前的两个潮流:一个是优化内容损失、一个优化感知损失。

2.2 Loss Functions

最常用的就是L2，优化它可以直接优化评估指标PSNR。近些年来，这个指标变成了L1，因为效果更好。但是总的来说，L1和L2指标和人肉眼关注的内容并不一致。另外的话，FSRNet用了一些其他的损失，比如landmark点以及解析图之类的回归损失。另一个优化方向是感知损失，这个指标与L2损失正好相反，目的是提升肉眼感官效果，但是却并不能显著的提升PSNR。

造成上述这种矛盾的一个原因在于，从LR到HR需要使用到学到的信息，但是在训练过程中，SR网络的核心功能“想象力”（特征字典或者映射图谱）会被L2/L1之类的损失函数限制（只有一个答案是对的，那就是HR!），从而导致最终我们看到的结果。

2.3 Generative Networks

介绍了ProGAN，styleGAN。具体细节不讲了，各位看两篇论文的原文或者论文的概括描述。

Section 3 方法

图给出了一个核心的内容 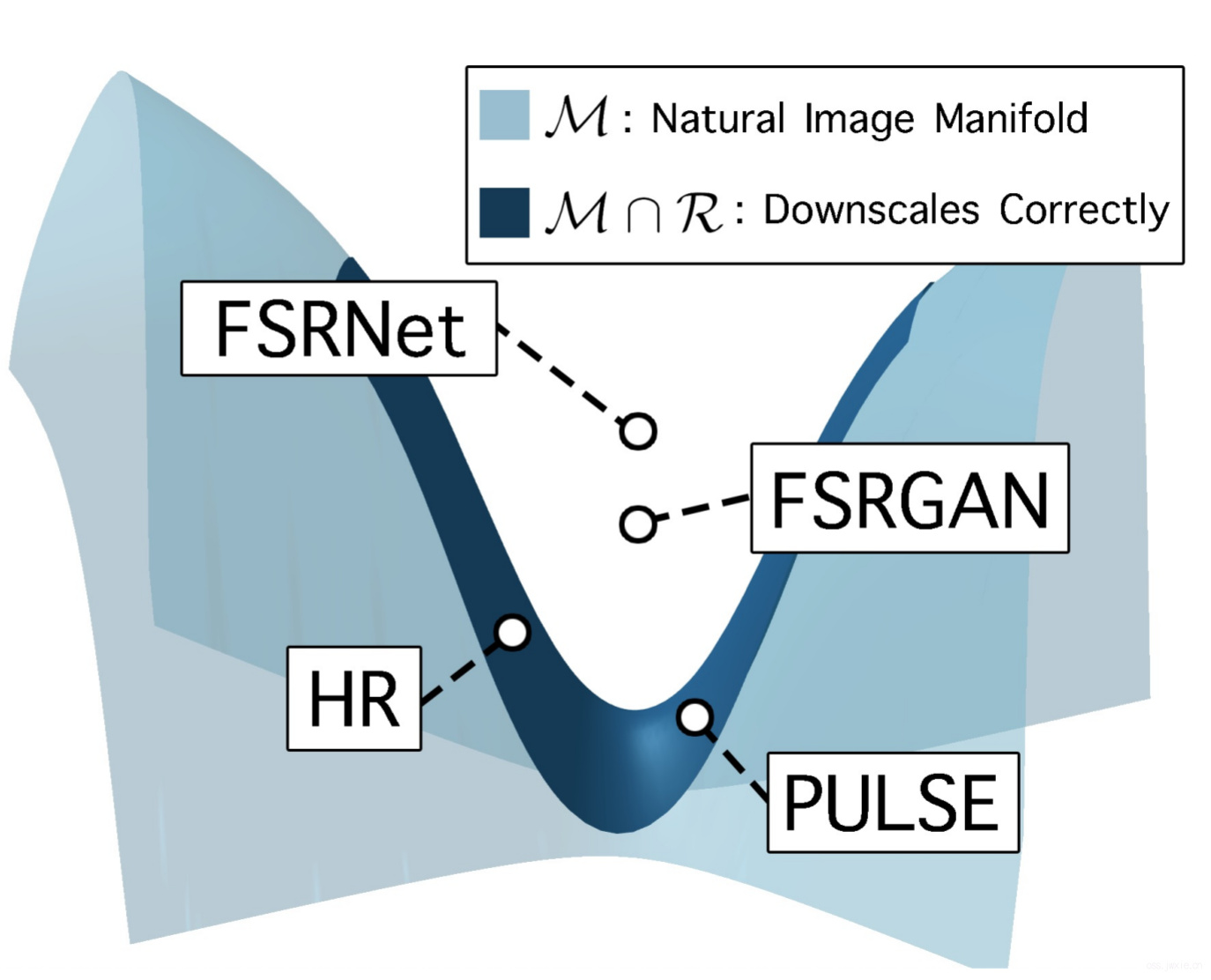首先定义一些术语：
\(I_{LR}, I_{LR} \in \mathbb{R}^{m \times n}\) 低分辨率输入图像
\(I_{SR}, I_{HR} \in \mathbb{R}^{M \times N}\) 超分辨率率网络输出图像
\(\mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{M \times N}\) 学到的映射关系
\(L:=\left|I_{H R}-I_{S R}\right|{p}^{p}\) 传统的内容损失的定义
\(\mathcal{M}\) 表明HR图像在\(\mathbb{R}^{M \times N}\) 中所对应的流形空间，其中数据集的概率分布，这个分布用\(P\)表示
\(R=\left\{I \in \mathbb{R}^{N \times M} DS(I)=I{L R}\right\}\) 表示正确下采样的一组低分辨率图像集合

然后我们来看为什么基于MSE的方法不太合适。当我们的而数据集趋向于无穷大的时候，网络输出的\(I_{SR}\)就会趋向于如下式: $$\int_{\mathcal{M} \cap R}\left|I_{HR}-I_{SR}\right|{p}^{p} d P\left(I{H R}\right)$$ 当\(p=2\)的时候，也就是采用MSE损失，上式的最小化就基于以下的条件:
$$I_{SR}=\int_{\mathcal{M} \cap R} I_{HR} d P\left(I_{H R}\right)$$ 这就导致了最优的\(I_{SR}\)变成了一个组高分辨率图像下采样后的低分辨率图像集合中所有图像中像素的逐像素加权平均的结果。

因此，我们这里提出了一个新的框架，设计了一个新的目标函数： $$\left|D S\left(I_{S R}\right)-I_{L R}\right|{p} \leq \epsilon$$ 其中要求\(\epsilon>0\)。 针对性的，我们设计了一个玩意儿\(\mathcal{R}{\epsilon} \subset \mathbb{R}^{N \times M}\)，让这个东西满足 $$\mathcal{R}{\epsilon}=\left\{I \in \mathbb{R}^{N \times M}:\left|D S(I)-I{L R}\right|{p}^{p} \leq \epsilon\right\}$$ 其实本质上就是采用一个合理的方式，将图像下采样到和\(I{LR}\)一样的大小，那么这就使得\(I_{S R} \in \mathcal{M} \cap \mathcal{R}{\epsilon}\)，也就是说 \(\mathcal{M} \cap \mathcal{R}{\epsilon}\)成为了一个可行解空间。同时，我们必然可以确定的是这个交集一定不会是一个空集合，因为原始的HR图像就处于这个集合中。

下图给一个实际上的可视化的内容，便于理解。

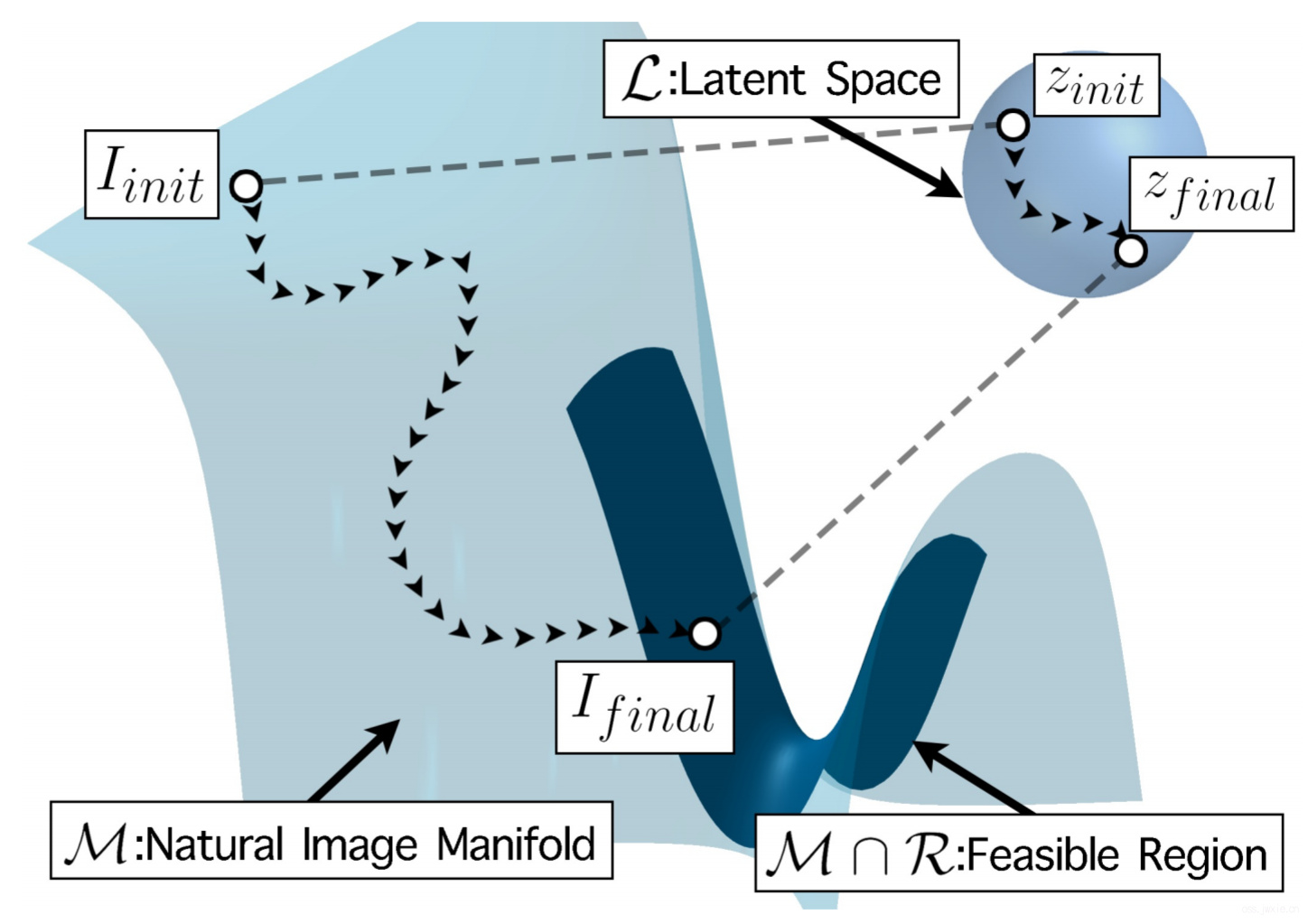
3.1 Downscaling Loss

仅使用\(L_p\)的方式来约束SR任务，实际上并不能保证我们能够逐渐趋近流行空间的目标区域。因此，在这个工作中，我们并不使用这种方式，我们是评估生成的图像和输入的低分辨率图像的相似度。

我们将其定义为下采样损失，这个想法实际上是基于一个设想：生成图像必须包含输入的低分辨率图像内所包含的所有信息，用公式来说:
$$I_{L R} \approx D S\left(I_{S R}\right)=D S\left(S R\left(I_{L R}\right)\right)$$ 其中\(DS\)是一个合适的下采样函数。然后按照这个说法，就可以有下面这个下采样部分的损失函数:
$$L_{D S}\left(I_{S R}, I_{L R}\right):=\left|D S\left(I_{S R}\right)-I_{L R}\right|_{p}^{p}$$

3.2 Latent Space Exploration

根据上面的描述，那么实际上我们只需要想办法把目标的流形空间进行可微分并参数化，那么依赖上面那个损失函数，我们就可以实现SR。同时，我们一定可以确保我们图像是高分辨率的，因为我们是在高分辨率的流形空间里进行定位。

可是，实际上这个参数化的流形空间并不好弄，但是我们可以使用无监督的方式来近似地对其进行参数化，大多数的生成模型都可以做到这一点。比如，我们从latent space\(\mathcal{L}\)中找到一个特征向量\(z \in \mathcal{L}\)，从而使得： $$\left|D S(G(z))-I_{L R}\right|_{p}^{p} \leq \epsilon$$ 另一个难搞的事情是单纯的从\(\mathcal{L}\)找到特征向量并不能保证得到我们想要的结果，这里还需要一个确定的先验。那解决方案也很简单，加一个小损失函数，其他人也是这么解决的[1]。但是这里作者提到了一个说法是，高密度的区域通常分布在以\(\sqrt{d}\)为半径的球面附近，那么为了靠近这个区域，我们替换高斯先验为\(\sqrt{d} \mathbb{S}^{d-1}\)。

解决方案GET，让\(\mathcal{L}^{\prime}=\sqrt{d} S^{d-1}\)，其中\(S^{d-1} \subset \mathbb{R}^{d}\)是一个\(d\)维欧几里得空间中的单位球面。然后，随机梯度下降的任务就变成了从全局的\(\mathcal{L}\)中找特征向量，变成了从局部的\(\mathcal{L’}\)中去找，任务顿时轻松多了😄。

Section 4 实验

速度不是很快，V100上~5s一张图像。

4.1 Data

数据集用的CelebA HQ。用了别人的StyleGAN预训练模型，然后将输入图像生成到1024x1024的大小，最高可以放大到64倍。

4.2 Qualitative Image Results

看图不说话，感觉是不错啊。

4.3 Qualitative Comparison

表格这边就不写了，实际不难懂。

4.4 Image Sampling

没啥好讲的。

Section 5 Robustness

尝试了不同程度的退化函数，效果如上图。

Section 6 Discussion and Future Work

  1. 基于GAN的模型虽然效果还不错，但是我们不一定能保证能覆盖完整的流形空间。
  2. 很多时候退化函数是已知的，因此我们的无监督的方法虽然可以取得不错的效果，但是可能有些冗余（不知道是不是该这么理解）。但是文章也提到了，使用基于训练的方法是可以估计退化模型产生的误差分布。

Section 7 Conclusion

没啥好说的

Reference

[1] Ashish Bora, Ajil Jalal, Eric Price, and Alexandros G. Dimakis. Compressed sensing using generative models. In Proceedings of the 34th International Conference on Machine Learning (ICML), 2017.