ResNeSt: Split-Attention Networks
🔗 PDF Link 🍺 Github Code
Attention是个好东西。😄
Section 1 介绍
分类网络结构是其他大多数任务的网络设计的基础。基于骨架网络,许多其他任务使用了如金字塔模块或者long-range连接,又或者是跨通道的特征图注意力机制来提升特定任务下的模型性能。
这就引出了一个问题:能否可以创建一个全能的网络,提升特征提取过程的性能,从而实现对所有任务的优化。
近期许多分类任务模型的提升主要是着眼于group/depth-wise卷积,这些方法虽然有效提升了性能和计算效率,但是从特征泛化性的角度去看,这些模型还不是很优秀。很久之前就有文献证明了,跨通道的特征信息提升各项下游任务的性能的基石。因此,加入跨通道的特征提取模块是分类任务中亟待解决的一个问题。
主要贡献:
- 探索了ResNet的结构改进,将特征图split attention融合进了一个独立的网络block中。简单来说就是按通道分组,然后对不同组的特征加权生成最终的特征表达。这种基于ResNet的block的改变,起了个名儿,就叫ResNeSt(S是split的意思)。
- 对下游的应用类任务进行大量的benchmark测试,发现提升了不少性能(具体这里不列举,后面有详细表格数据)。
Section 2 相关工作
Modern CNN Architecture
Network in Network 第一个使用全局平均池化(GAP)代替全连接层来进行非线性整合。
VGGNet 提出加深网络深度,堆叠blocks来提升性能。
Highway Network 提出highway连接,促进了层间特征信息的流动,辅助收敛。
基于前面几个网络,ResNet提出identity skip连接,缓解了梯度消失,是的网络可以堆 得更深,特征层次更丰富。
Multi-path and Feature-map Attention
多路(Mutli-path)的特征提取在GoogleNet中已经显示出了卓越的性能,紧接着ResNeXt采用的组卷机,将这种多路卷积转变成一个个独立的小卷积。
SE-Net引入了通道注意力机制,利用GAP自适应地对特征图重新加权整合(校准)。
SK-Net引入了多路特征(不同的kernel大小),然后使用类似SE-Net的方式对split后的特征进行融合。
NAS
计算能力的提升使得可以有机会试用网络搜索的方式来实现网络结构设计,近期的网络结构设计如AmoebaNet,MNASNet,EfficientNet都是这方面的一些尝试。但是这么做虽然可以获得一个性能优异的网络结构模型,但是也存在着一定的劣势,这些搜索出来的网络结构在一定程度上是很难被应用到后续的下游任务中去的。但是,本文的工作实际上倒是给Design Space增加了一个选择方案。
Section 3 Split-Attention Networks
整体的结构如下图第三张图所示。
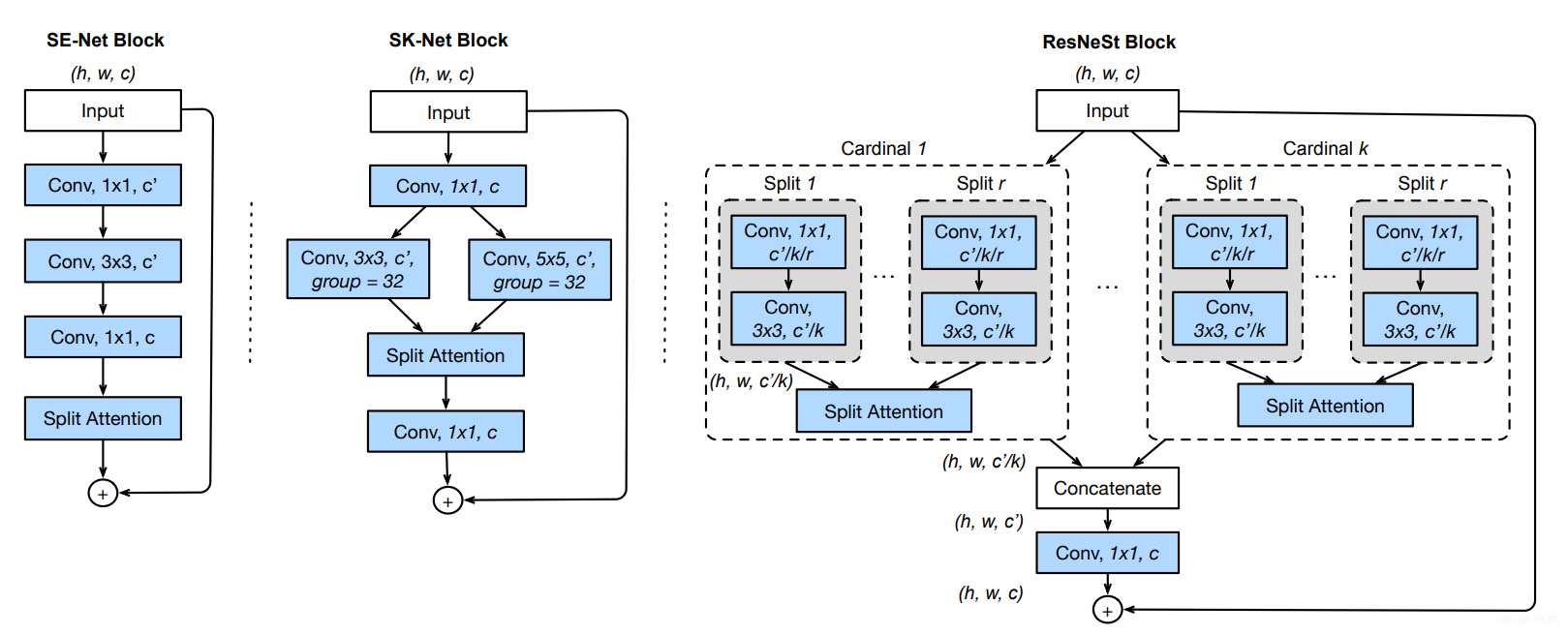
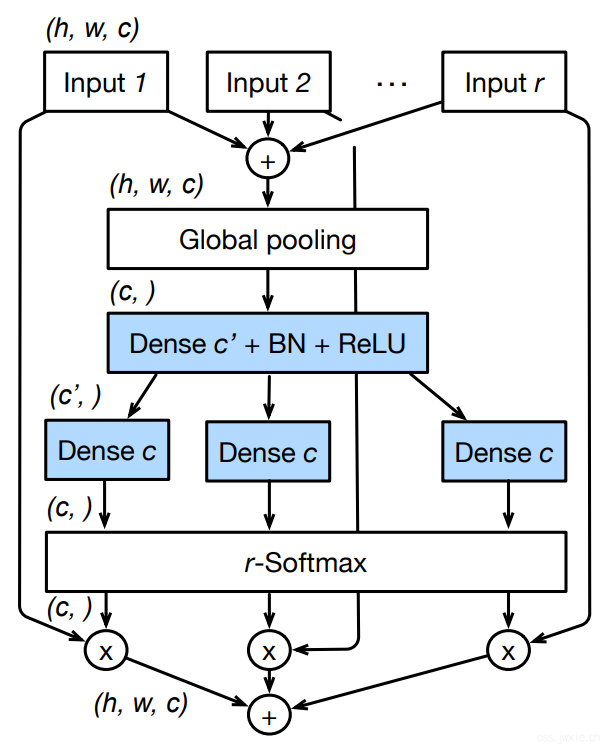
下图细节展示了每一个cardinal中的具体结构。
Feature-map Group
定义了两个参数\(K\)和\(R\),前者是控制有多少个path(s),后者是控制每个path里面有多少个split(s)。这就造成了一共有\(G=KR\)个groups,针对\(G\)组,每一组都可以应用一个transformations,然后想一些办法把他们产生的特征图整合起来(特征融合Fusion😄)。
Split Attention in Cardinal Groups
根据上面的是说法和[1,2]两篇文献,整合起来的特征表达可以由多个跨通道的group(s)产生的特征图逐像素加融合(Fushion)而来,整合方式的话就可以使用GAP(全局均值)来进行加权嵌入。
下面顺着公式和上图具体讲一下整体的流程。
- 确定每一个cardinal的输入 \(\hat{U}^{k}=\sum_{j=R(k-1)+1}^{R k} U_{j}\),具体的根据前文的描述,每一个cardinal都可以分为好几个split(s),每一个split的输入实际上就是cardinal输入的一个子集。
- 然后对每一个cardinal中的每一个split所分到的输入而言,使用SE-Net和SK-Net里面所提到的Attention思想,使用GAP来算权值。 $$s_{c}^{k}=\frac{1}{H \times W} \sum_{i=1}^{H} \sum_{j=1}^{W} \hat{U}_{c}^{k}(i, j)$$
- 用下面的式子对算出来的权重进行soft重排(个人理解就是为了限制一下权重的范围,使得更好理解呗,有点像SE-Net最后那个实验,可视化权重的那个)。
$$ a_{i}^{k}(c) = \left\{ \begin{matrix} \frac{\exp \left(\mathcal{G}{i}^{c}\left(s^{k}\right)\right)}{\sum{j=0}^{R} \exp \left(\mathcal{G}{j}^{c}\left(s^{k}\right)\right)} & \text { if } R>1 \\ \frac{1}{1+\exp \left(-\mathcal{G}{i}^{c}\left(s^{k}\right)\right)} & \text { if } R=1 \end{matrix}\right. $$
-
那么利用前文提到的逐像素的融合的方法,每一个cardinal的输出就变成了 $$V_{c}^{k}=\sum_{i=1}^{R} a_{i}^{k}(c) U_{R(k-1)+i}$$
-
其中, \(a_{i}^{k}(c)\) 代表的就如上上个公式所展示。具体的看,当只分一个split的时候,就是一个简单的sigmoid函数;而当分出多个splits的时候则是使用了类似softmax的形式。(这里实际上还有点疑惑, \(G\) 到底是个啥,功能是根据上下文信息来给出权重)
然后就可以得到我们想要的ResNeSt Block了,配合上Residual的思想,我们把 \(V=Concat(V^1, V^2, V^3, …, V^k)\) 看作是每一个cardinal的拼接结果,然后针对每一个Block, \(Y=V+X\) 当然,存在着前后输入和输出的特征图大小不匹配的情况,那么公式就变成了\( Y=V+\mathcal{T}(X) \) 用以匹配前后的特征图尺寸。具体的看,实际上这写cardinal中的卷积完全都可以使用一些标准化的卷积层(例如组卷积之类的),本质上ResNeSt的参数两和ResNet不相上下(同尺寸,同规模的情况下)。
Section 4 Network and Training
这里就讲一些小技巧了。
Network Tweaks
- Average Downsampling
这里也讲到了zero-padding会到之性能缺失,这个点其实蛮重要的。 - Tweasts from ResNet-D
(1)用3个3x3卷积替代一个7x7卷积(这个老生长谈了)。
(2)加了一个2x2的average pooling到skip connection里去。
Training strategy
Large Mini-batch Distributed Training
Label Smoothing
Auto Autoaugmentation
Mixup Training
Large Crop Size
Regularization
Section 5 Image Classification Results
Section 6 Transfer Learning Results
上面两章节都是实验的结果部分的展示,咋说呢,重点是思想,结果不重要 😄。
Section 7 Conclusion
提出了Split-Attention-Block效果很棒。
Reference
[1] Hu, J., Shen, L., Sun, G.: Squeeze-and-excitation networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 7132–7141 (2018)
[2] Li, X., Wang, W., Hu, X., Yang, J.: Selective kernel networks. In: Proceedings
of the IEEE conference on computer vision and pattern recognition. pp. 510–519
(2019)