On Network Design Spaces for Visual Recognition
🔗 PDF Link 🍺 Github Code
RegNet前篇!😄
Section 1 简介
目前,在Visual Recognition领域里,网络结构搜索的一系列工作就类似在进行着“随机梯度下降”,每次提出新的模型结构都像是在无限维度的解空间里朝着“最优解”方向走了一个step。(这话讲得真没错啊!!!😄)。
既然类似于GD,那么对应着我们要朝着最优(时间、精度之间tradeoff,多任务、数据集的泛化性能等多项指标都要经得住时间的考验)的方向走,必须要有一个优秀的“损失函数”来告诉我们是否当前新提出的模型比以前的更好。
对此,一个比较好的思路是先对NN有一定的理论理解之后,从而构建新的网络结构,但这个过程具有一定的滞后性(必须等待新的理论的发现才能取得新的进步)。那么一个新的思路在于使用经典统计学,即在没有General理论研究发现的前提下,通过一些统计实践研究来确定论证结论。(害,感觉不都是这么做的嘛😄)
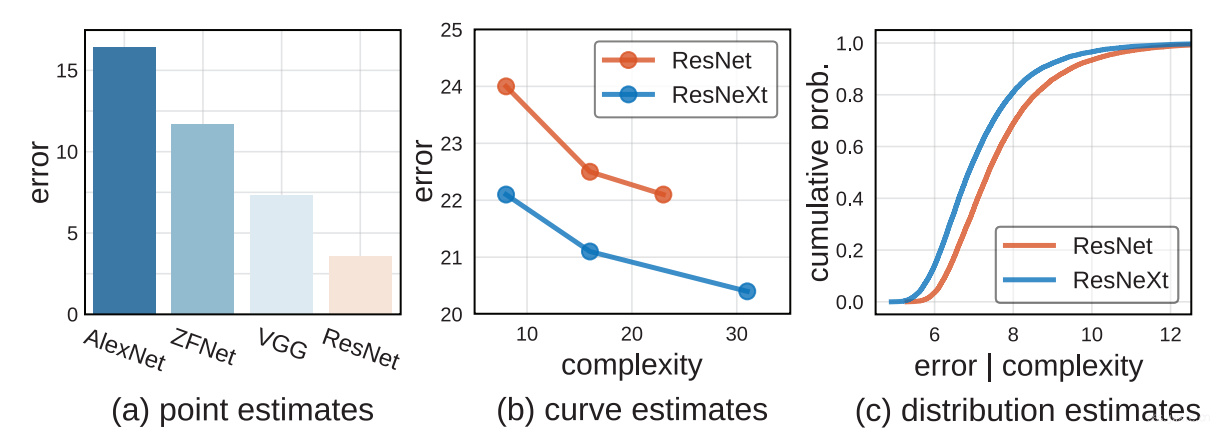
如上图,实际上一些工作也是这么做的(整体趋势如此),以下给出了三个方向。
- Point estimation,即新提出的模型的性能点比别人更高(或者错误率更低)那么新模型就是更优的。比如(a)里,在Benchmark里,有更低的错误率就表明模型更优秀。
- Curve estimation,即通过实例化新提出的模型(model family),跟踪错误率和模型复杂度之间的关系来构成的曲线。比如(b)里,曲线中每一个点都取得较之前的模型更低的准确率才能证明新模型更优。但是,这里有个问题就是,曲线里面并非所有的点(每一个点其实就是model families中的一个model,表明新模型的一个实例)都有一致的混杂因素(confounding factors)。
个人理解:是否是说这些曲线中的点并非标准的对照试验,而是由多个超参数调节的前提下,曲线估计才能做到最优。
这个曲线估计(变动单个超参数才生成曲线,比如光换宽度,固定深度等其他因素)的评估方式其实提示了一种通用的方法,即变动所有与模型性能相关的超参数。原则上看,这种情况实际上将会消除model families里混杂因素所产生的影响,但是这种情况造成了一个问题:又有可能产生大范围(有时候通常是无限的)可能性空间。在没有特定约束的前提下,可行性是存疑的。 - Distribution estimation,如图(c)。与前面提到的近对比一部分model families不同,直接从设计空间中抽样可能的参数化结构,然后对错误率和模型复杂度的分布进行估计。然后根据曲线,采用一系列的统计方法对这些分布(设计空间)进行比较优劣,与前面两个估计方法相比,这种方法更完整、更公正。
为了验证这个方式是否正确,文章在CIFAR上训练了超过10000个模型(真变态…)。这些模型的训练为的就是能更好的模拟分布估计并得出鲁棒的结论。但是,实际上跑100-1000个模型就足以支撑一个可靠的估计了。后续在ImageNet上也进行了同样的验证,证明了这个方法在特定环境下是feasible的,也可以用来去辅助探索新型的网络结构。
为了做案例研究,做了一些关于NAS的调查,探究一下NAS的设计空间,发现不同的NAS所使用的设计空间存在着巨大的差异。这里文章假设了正是这种差异导致了这些模型存在着性能提升。此外,文章还证明了即使是采用标准的ResNeXt的设计空间,实际上也可以和近期提出具有超复杂设计空间的NAS相媲美。✨这么屌的么✨
从本质上看,这篇文章的工作就是对NAS的一个补充。NAS是在一堆model fanlilies里找到一个best。而文章的工作则在于找到model fanilies的特征。换句话说,怎么去设计设计空间。
我们注意到我们的工作是对NAS的补充。 NAS专注于在给定的模型族中找到单个最佳模型,而我们的工作着重于描述模型族本身的特征。换句话说,我们的方法论可以使人们能够研究设计用于模型搜索的设计空间。
文章会公布所有的模型、代码和统计信息以供验证。
Section 2 相关工作
⭐ 细节自己看奥 ⭐
- Reproducible research –> 害 大家做这行的肯定要注重一下可复现性+鲁棒性嘛。
- Empirical studies –> DN缺乏严格的理论依靠那必要就要进行大规模实验,实际上经典模型的可探索性是极强的[1,2]。
- Hyperparameter search –> 通用超参数搜索在实践中存在一定挑战, 随机搜索能提供更好的baseline和可重复性。
- Neural architecture search –> NAS=设计空间+设计空间搜索(RL,启发搜索,梯度搜索,进化算法),前者却很少。
- Complexity measures –> ML实际引入了网络复杂度的概念,但是这很难预测NN的结果,更常用的却是参数量或是FLOPs。
Section 3 设计空间
3.1 定义
I. Model familiy
模型族是一系列NN结构(可能不一定是一系列,有可能是无限的一个collection)。举个例子来说有两个方向,标准的前馈网络ResNet或者是NAS。
II. Design space
进行这类model family的研究相对是比较困难的,主要难点在于范围太过庞大。实际上,我们需要对抽象model families和design space做出一定的区分。**实际上design space是可以从model family中实例化的一部分具体的结构集合。**具体的,其实可以分成两个部分,一个是参数化的model family(一系列参数,通过这一系列参数可以完整的定义一个可以实例化的网络),另一个是参数池。
III. Model distribution
为了验证研究的性能,实例化每一个模型是不成的😄。因此嘛,文章从design space里采样了一部分模型,并用这部分模型的实例化结果作为多次抽样的结果,然后利用统计学方法来做出判断。
IV. Data generation
具体的看后面的,这里没说啥。
3.2 实例化
I. Model familiy
文章探究了三个families,“vanilla”, “ResNet”,“ResNeXt”。
II. Design space
具体的,文章把整个网络分成了三个部分stem/3 stages/head。具体的,每一个stage可以涵盖多个blocks,如下表。
| stage | operation | output |
|---|---|---|
| stem | 3×3 conv | 32×32×16 |
| stage 1 | {block}×d_1 | 32×32×w1 |
| stage 2 | {block}×d_2 | 16×16×w2 |
| stage3 | {block}×d_3 | 8×8×w3 |
| stage 4 | pool + fc | 1×1×10 |
- ResNet的design space中每一个block都是两个3x3的卷积和一个残差链接。
- Vanilla的design space中用了一个identical block但是没有残差❓。
- ResNeXt的design space中用了bottleneck blocks with groups,对此产生了两个变体ResNeXt-A和ResNeXt-B,如下表。
| depth | width | ratio | groups | total | |
|---|---|---|---|---|---|
| Vanilla | 1,24,9 | 16,256,12 | 1,259,712 | ||
| ResNet | 1,24,9 | 16,256,12 | 1,259,712 | ||
| ResNeXt-A | 1,16,5 | 16,256,5 | 1,4,3 | 1,4,3 | 11,390,625 |
| ResNeXt-B | 1,16,5 | 64,1024,5 | 1,4,3 | 1,16,5 5 | 52,734,375 |
III. Model distribution
如上表,从中抽样。其中total表示一共可以供抽样的模型数量。
IV. Data Generation
文章一共抽样、训练了100k个模型。为了减少计算负担,文章并不考虑FLOPs和参数量大于ResNet-56的模型。
Section 4 方法
4.1 分布对比
采用point estimate,可以对一个新提出的网络进行参数的网格、人工搜索。但实际上这种基于点估计的评估方式有一定的误导性,举一个简单例子来说:假设我们现在两个有着不同大小但是是从同一个设计空间中采样出来的模型集。
-
点估计。
采用随机搜素的方法,首先通过均匀采样100个结构(在ResNet的设计空间中),生成一个baseline(B)。然后,为了生成第二个模型集(M),却需要采样1000个结构。 –> 这里没太看?训练完成后,由于M的最小损失比B低,因此我们得出一个naive的结论:M更好。那么回过头来看实际情况,文章对这个设计空间进行了更多次的采样,得出了下图左边的部分。
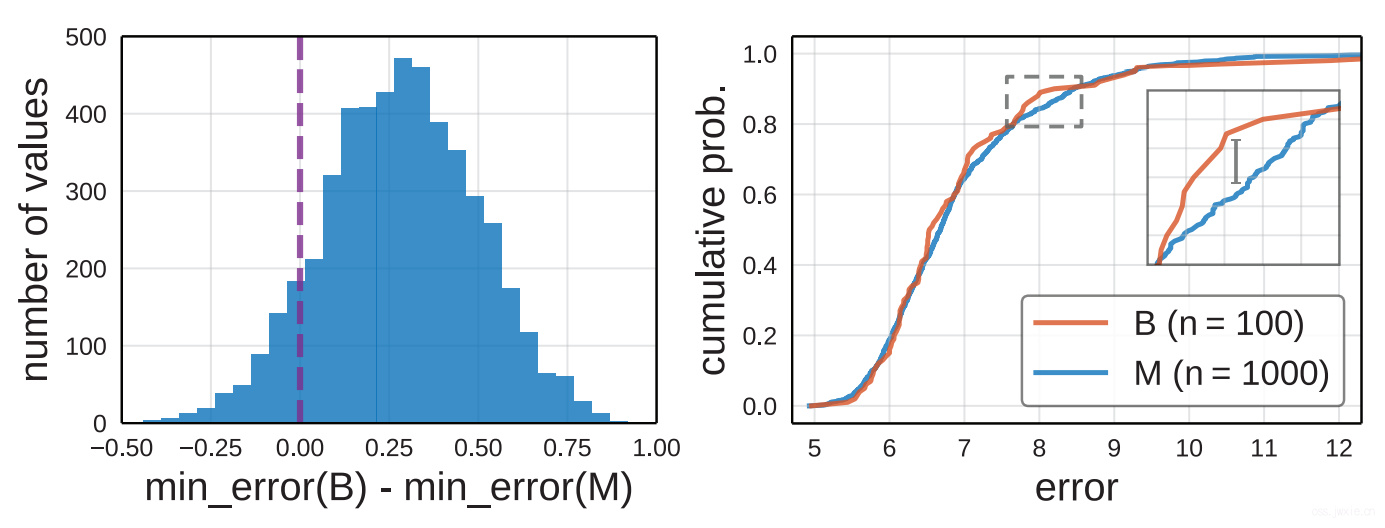
从上面这张图上看,实际上是在~90%的情况下,M会比B更好一些,但实际上这两个模型是来自同一个设计空间的。这么看来点估计实际上存在一定的误导性。
-
分布。
文章的工作中采用了分布来取代点估计,通过直接对比分布,可以以此得出更加鲁棒的结论。
对此,这里使用了empirical distribution functions(EDFs),如下式。 $$F(e)=\frac{1}{n} \sum_{i=1}^{n} \mathbf{1}\left[e_{i}<e\right] \tag{1}$$
其中,\({e_i}\)表示\(n\)个模型中的错误率,\(\mathbf{1}\)是一个指示函数。这么来看其实\(F(e)\)就像是一个两个模型对比的中,一个模型优于另一个模型的一个比例。再次回过头来看,上图的右边那部分就是一个EDFs的典型案例。 定量的来看,文章是在同一个设计空间中进行采样的两个模型,因此实际上可以使用两样本的KStest[3]来检验是否这两个模型的结果出自同一分布,具体的如下式: $$D=\sup_{x}\left|F_{1}(x)-F_{2}(x)\right| \tag{2}$$ 其中\(D\)是KStest,\(F_1\)和\(F_2\)表示的是两个模型的EDFs。结合上图的右边半张图中放大展示的那部分很小的差异,以及检验结果\(D=0.079, p=0.60\)来看,无法推翻原假设,即B和M应该来自同一个分布。
-
讨论。
⭐ 语重心长教育我们要用分布,而不是点估计。 (害,你把卡给我跑跑呗,哥 😂)
4.2 控制模型复杂度
尽管通过对比分布可以得到更鲁棒的结论,但是实际上在进行对比的时候,还是需要控制一下confounding factors,比如这里的模型复杂度。
-
Unnormalized comparison
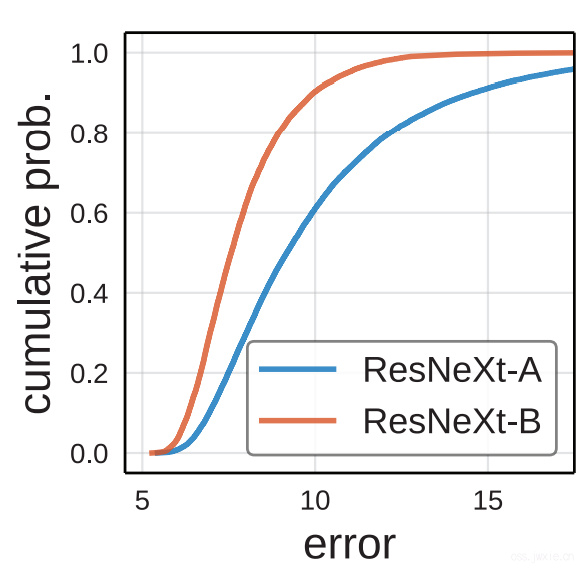
在不加限制的条件下,上图展示了ResNeXt-A和ResNeXt-B两个设计空间,具体的如第三章里的第二张表所示。这种明显的差异表明,在相同模型分布下,来自同一个model family的不同设计空间可能会导致不同的错误分布。
(注:这里讲一下这个图到底啥意思,横坐标就是错误率的阈值\(e\),纵坐标表示累计概率,其实就是占比,如式(1)) -
Error vs. complexity
实际情况中,我们知道在多数情况下,更复杂的模型能取得更好的准确率。
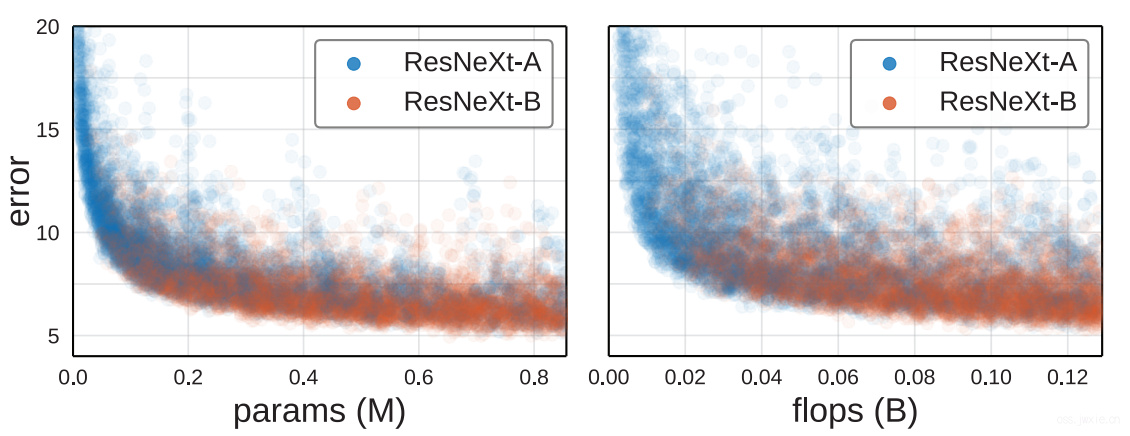 文章探究了这个结论,结果如上图所示。通过参数量和FLOPs来衡量复杂度,尽管有部分高复杂度模型有较差的结果,但是最低的错误率模型(best model)的复杂度也是最高的。目前为止,这个结果没有达到饱和的迹象。
文章探究了这个结论,结果如上图所示。通过参数量和FLOPs来衡量复杂度,尽管有部分高复杂度模型有较差的结果,但是最低的错误率模型(best model)的复杂度也是最高的。目前为止,这个结果没有达到饱和的迹象。 -
Complexity distribution
现在回头去看之前在[Unnormalized comparison]部分提到的那张图,那张图的记过是否是因为ResNeXt-A和ResNeXt-B之间有复杂度的差异所导致的呢?由此可以将复杂度纳入到考虑因素中去,得到下面两个结果。
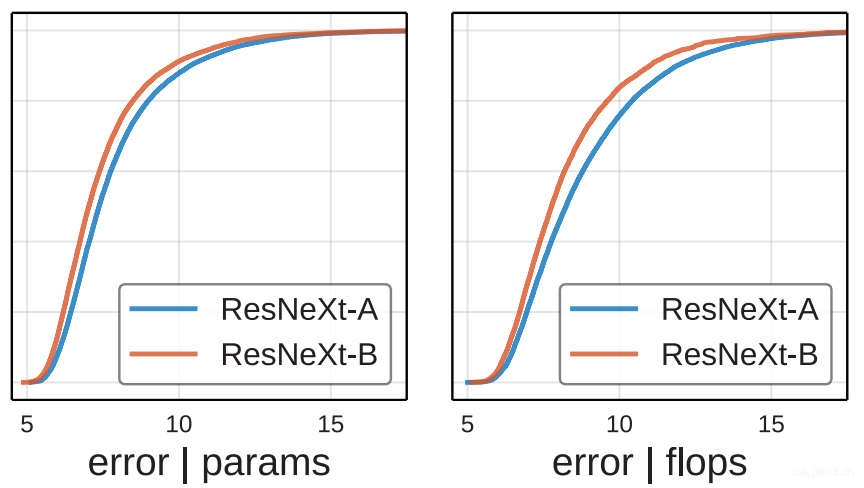 从这个结果看,其实不免可以得出的结论是ResNeXt-B的性能有可能就是由于复杂度高所产生的。
从这个结果看,其实不免可以得出的结论是ResNeXt-B的性能有可能就是由于复杂度高所产生的。 -
Normalized comparison
文章提出了一种归一化流程用于排除复杂度在模型分布中的影响。考虑\(n\)个模型,其中模型复杂度为\(c_i\),给每一个模型一个权重\(w_i\),使得\(\sum_{i} w_{i}=1\)。那么,这样的话\(n\)个模型就有\({e_i}\),\({c_i}\),\({w_i}\)三个变量,对应的新的标准化复杂度 EDF就可以如下式: $$C(c)=\sum_{i=1}^{n} w_{i} \mathbf{1}\left[c_{i}<c\right] \tag{3}$$
标准化错误率 EDF如下式: $$\hat{F}(e)=\sum_{i=1}^{n} w_{i} \mathbf{1}\left[e_{i}<e\right] \tag{4}$$那么剩下的事情就很方便了,只要我们在两个给定的模型集上,尽可能的使\(C_{1}(c) \approx C_{2}(c)\),这样的话,\(\tilde{F}{1}\)和\(\hat{F}{2}\)的比较就消除了模型复杂度因素。
实际上,在为每个模型设置权重的时候(为了使得复杂度一致),文章将复杂度的范围分成了\(k\)个小bins,然后对每一个落入第\(j\)个小bin的模型\(m_j\)设定权重为\(w_{j}=1/k m_{j}\)。尽管存在这其他方法来达到同样的效果,但是文章这里发现同时对\(C1\)和\(C2\)一起整还是挺有效的。(有点不清楚咋整的💔)
在上图中,可以发现的经过复杂度归一化后,两个曲线很接近,这个是在意料之中的,毕竟来自同一个设计空间。但是,另一个问题是,尽管如此他们之间依旧存在着一些小小的gap。这可能是由于ResNeXt-B的设计空间可能更宽,而且groups更多。
4.3 分布化
这种类型的研究,一个很大优势在于,他不仅可以给你什么模型有着最小的误差率,而是能给你在什么情况下(不在局限于一部分参数的变动),能获得最小的准确率。
-
分布形状
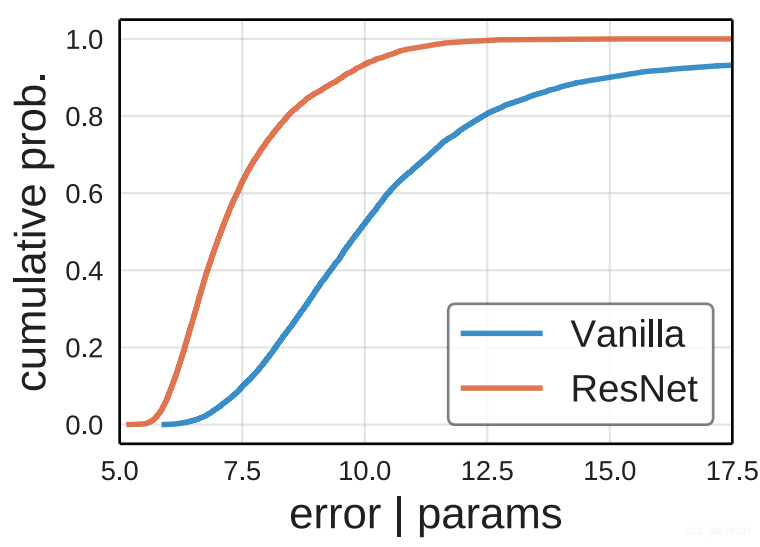
上图展示了Vanilla和ResNet的设计空间下的EDFs。ResNet有>80%的模型有着<8%的错误率。与之相对比,Vanilla仅有~15%的模型错误率<8%。尽管这点毋庸置疑(ResNet就这么吊呀),但是这的确反映了了可以从这个分布图中看出一些模型错误率以外的东西。 -
分布面积 跟AUC一样,实际可以对EDFs的曲线下面积进行计算来评判到底哪个design space更好,计算公式如下: $$\int_{0}^{\epsilon} \hat{F}(e) / \epsilon \mathrm{d} e=1-\sum w_{i} \min \left(1, \frac{e_{i}}{\epsilon}\right) \tag{5}$$
万分注意! 其实光看面积来比较模型也是不太对的,毕竟只是一方面! -
随机搜索的效率 评估是否容易找到一个模型的另一个方法在于随机搜索的效率。 <😂这里不太懂… 是否意思就是更容易搜到的模型更符合奥卡姆剃刀原理?>
文章这里用的办法就是的[4]方法。比如实验的大小是\(m\),对应着我们要从\(n\)个模型池子中抽样\(m\)个然后算最小误差。大约重复\(n / m\)次,然后用式3的方法排除模型复杂度。
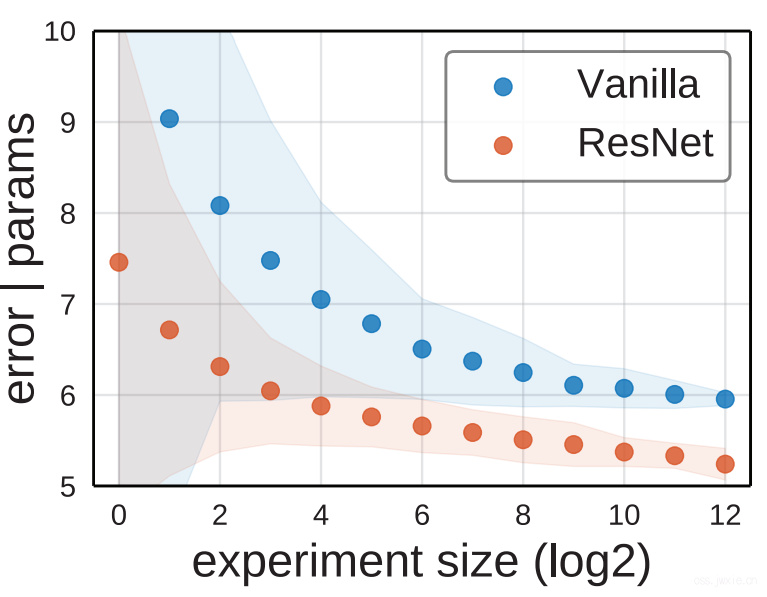
然后就可以得到上图的结果(这张图的意思大概是说,到达预定所需要的错误率|参数量所需要的随机搜索次数的对比 –> 但是,实际上这张图是通过变动\(m\)来看对应产生的模型最小错误率画出来的。😂是真狠…)。
4.4 最小采样大小
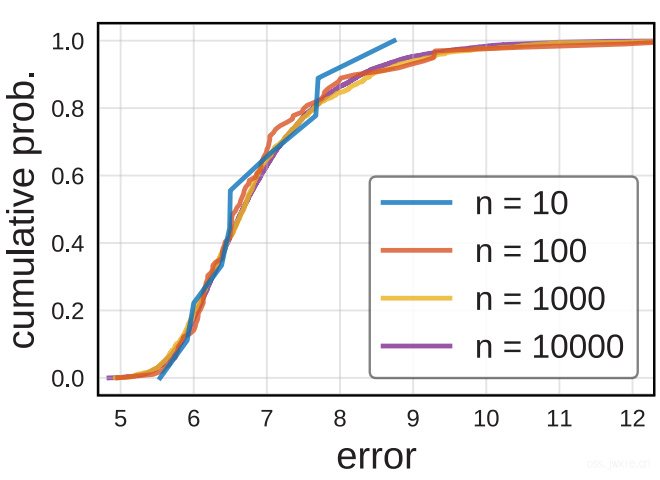
-
定性分析 上面那张图展示了ResNet在不同的采样大小下的EDFs。10次抽样的结果有太多的噪声了,100的时候有已经很理想了,1000和10000次基本差别不大。文章这里说大概100次就够了。
-
定量分析 一样的方法,用KStest(Eqn. )来做定量分析。
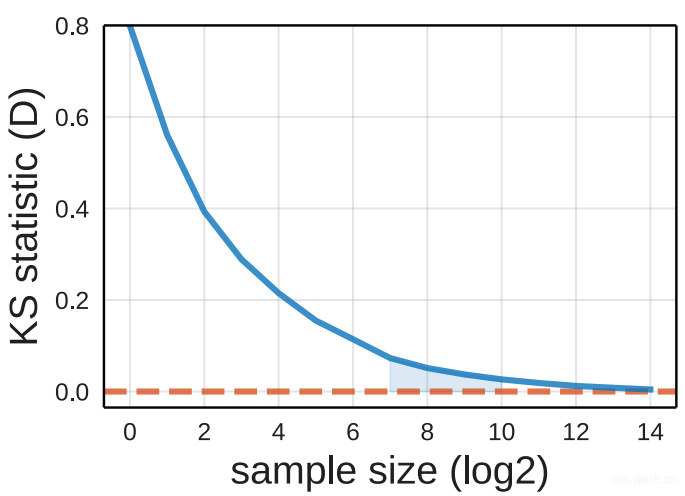
如我们所想的一样,随着\(n\)大小上升,\(D\)也随着降低。100次的时候大约0.1,1000次接近饱和,超过1000次之后基本收益也么得了。所以100次足够,1000次精度更高,在往上也没啥必要了。 -
可行性讨论 有人肯定在想了训练100-1000次网络的效率(没错就是我😂)。在文章中训练500个CIFAR模型,需要250 GPU hours,而在ImageNet上训练ResNet-50的baseline就需要192 GPU hours。这么看来在CIFAR小规模上进行探索就与探索一次ImageNet所需要的时间相等了。但是在NAS上,CIFAR问题就肯能需要\(O(10^5)\)GPU hours。因此文章希望这种方法可以成为一种典型分析方法,同时也公开了所有的数据作为后续工作的参考。
Section 5 案例研究:NAS
NAS有两个关键部分,搜索空间和搜素算法,但是多数人都关注与后面的那个。文章发现好多的近期的NAS文章中的设计空间的巨大差异被大家忽略了。
5.1 设计空间
-
I. Model family NAS实际上是堆叠各类单元(cells),并采用不同的堆叠方式来实现的,具体的看ENAS[5]。
-
II. Design space 虽然近期很多NAS论文都采用了通用的NAS model family,但是新的工作都采用了不同的实例化设计空间。例如在,NASNet,AmoebaNet,PNAS,ENAS和DARTS中,cell的结构很本质的不同,如下表。
#ops #nodes #output #cells (B) NASNet 13 5 L 71,465,842 Amoeba 8 5 L 556,628 PNAS 8 5 A 556,628 ENAS 5 5 L 5,063 DARTS 8 4 A 242 文章这里采用了5种cell结构,NASNet,Amoeba,PNAS,ENAS,DARTS。
此外,如何去堆叠不同的cells,在近期的工作中的也存在着一些差异。这需要定义一些标准,这里就主要采用了DARTS[6]的方法。
深度\(d\)和宽度\(w\)保持固定,但是这俩参数直接影像网络的复杂度。
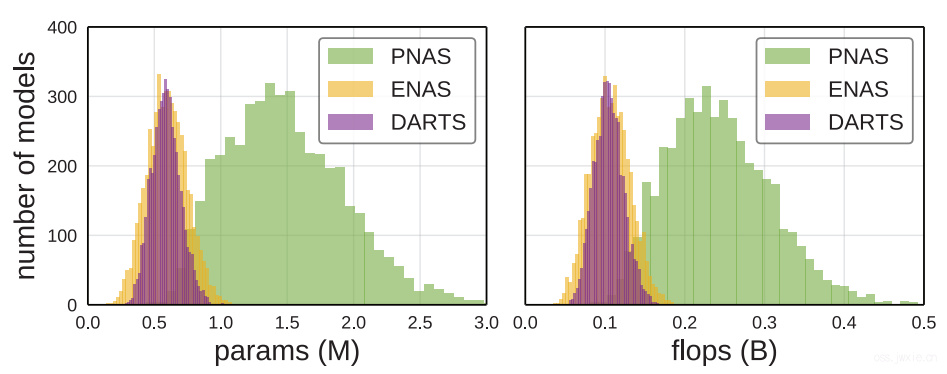
看上图,具有相同参数量的模型的数量分布图。所以,这里还是采用变动的\(w \in{16,24,32}\),\(d \in{4,8,12,16,20}\),以便于控制变量进行对比。
-
III. Model distribution 全部均匀采样!
-
IV. Data generation 训练~1k个模型,保证采样到了足够全范围的FLOPs和参数范围。
5.2 设计空间对比
-
分布对比
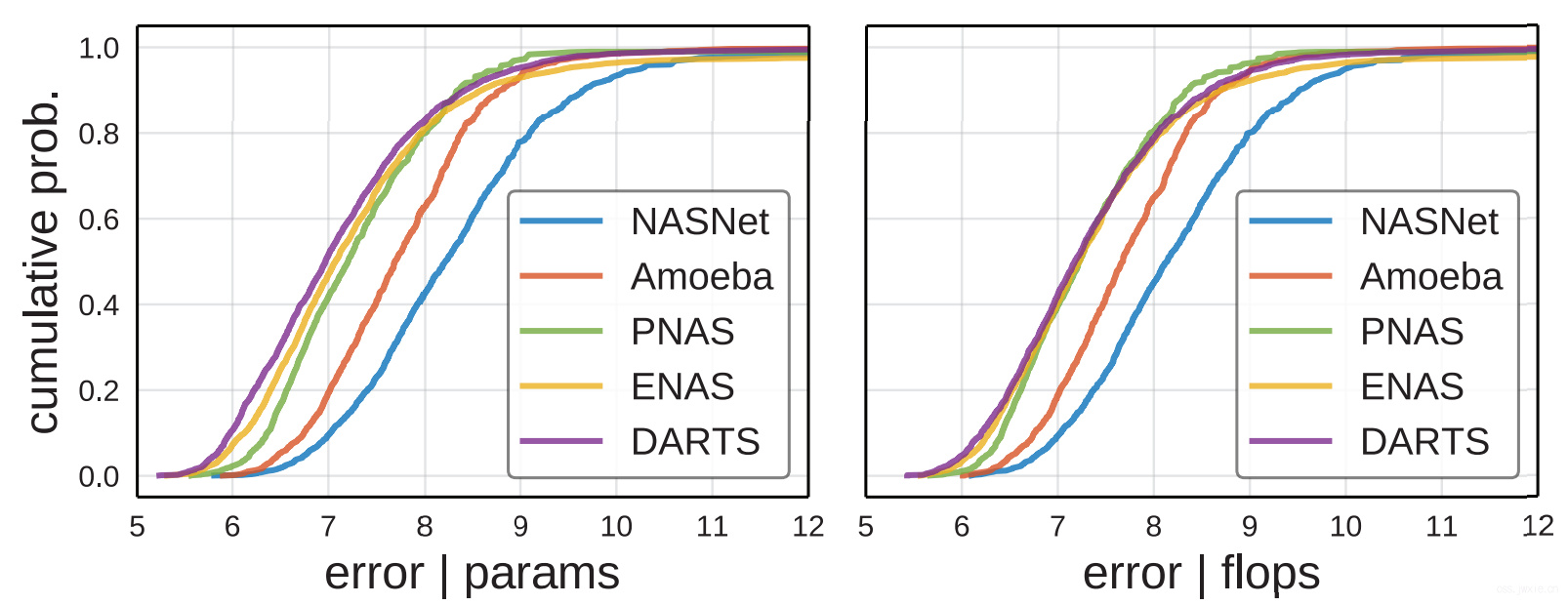
上图来看,各个方法的EDFs差异还是蛮大的,DARTS最好,NASNet和Amoeba明显弱于其他的。⭐剩下的细节的话自己看看。有趣的发现是,新提出的方法的设计空间明显有更好的性能。因此对前人的设计空间进行pruning是有一定的improvements。而且,新的工作也的确在design space上有一定的进步。
-
随机搜索效率
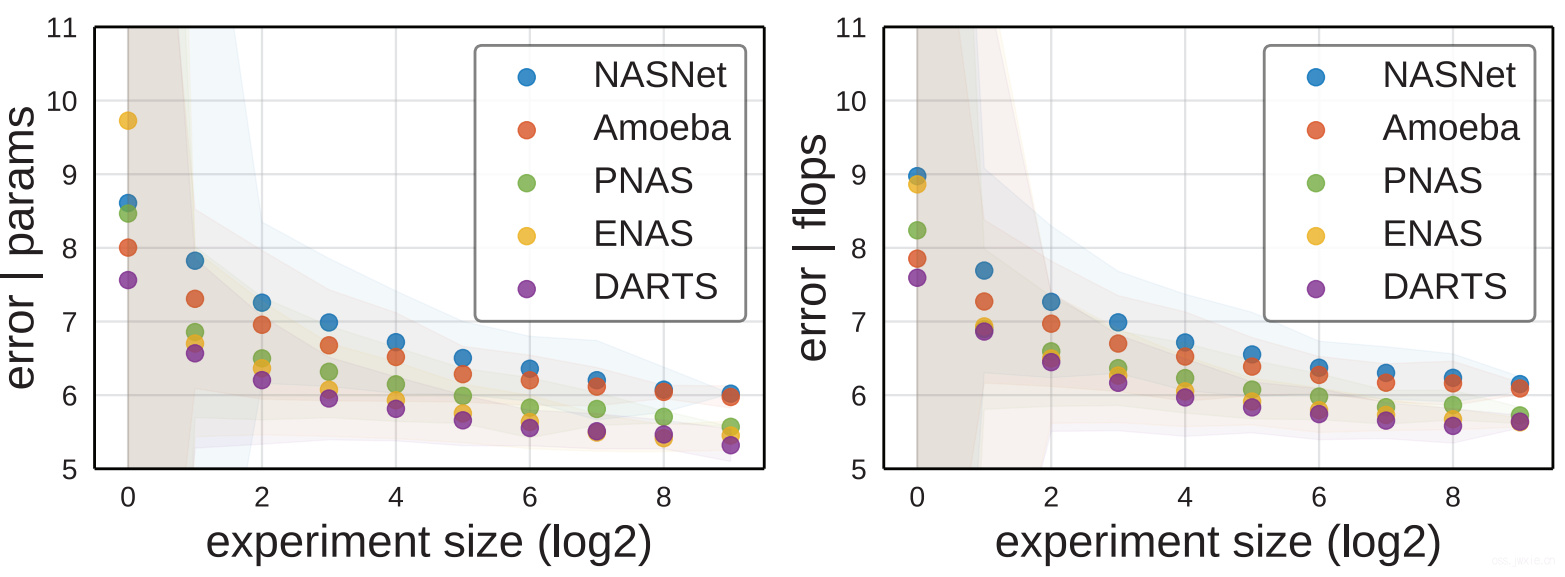
一样的方法来做,看上图,基本那结果排序与上面分布对比的结果类似。另外一个很重要的结论在于在对比搜索方法的时候,需要固定搜索空间相同(因为搜索空间的差异会导致最终性能产生明显差异)。
5.3 与标准设计空间对比
对比了一下ResNeXt-A,ResNeXt-B以及NAS的design space,结果如下图所示。
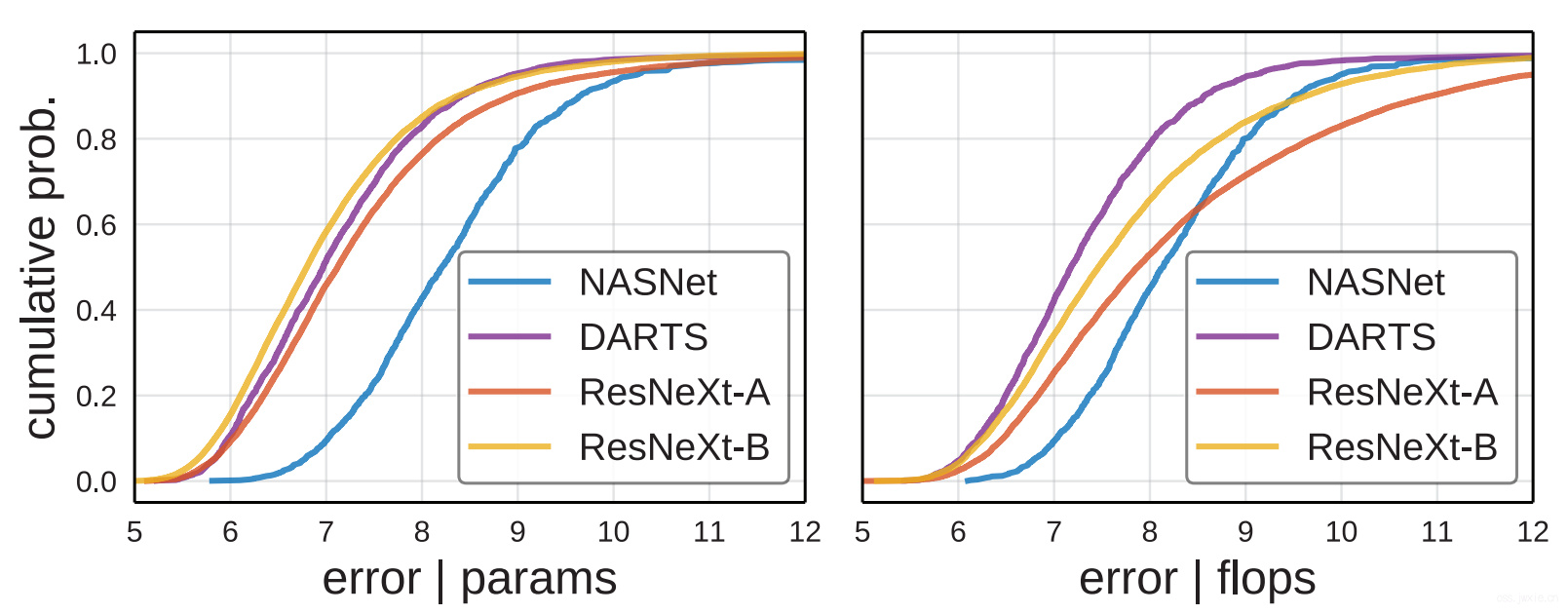
结果就很有意思了,这里发现实际上标准设计空间的性能并不比NAS差。并且,设计空间对模型性能的影响真的很大。
5.4 健全性检查
| flops (B) | params (M) | error original | error default | error enhanced | |
|---|---|---|---|---|---|
| ResNet-110 | 0.26 | 1.7 | 6.61 | 5.91 | 3.65 |
| ResNeXt⋆ | 0.38 | 2.5 | – | 4.9 | 2.75 |
| DARTS⋆ | 0.54 | 3.4 | 2.83 | 5.21 | 2.63 |
使用本文的方法实际上可以取得较好的性能表现,具体如上表所示。其中original是原始报道的错误率,default是默认网络框架下的性能表现,enhanced是搜索design space后的最小结果,基本你能提升~2%左右!!
Section 6 结论
文章提出了一种用于分析和比较模型设计空间的方法,这种方法可以广泛用于多个领域。
References
[1] G. Melis, C. Dyer, and P. Blunsom. On the state of the art of evaluation in neural language models. In ICLR, 2018. 2
[2] S. Merity, N. S. Keskar, and R. Socher. Regularizing and optimizing lstm language models. In ICLR, 2018. 2
[3] Frank J Massey Jr. The kolmogorov-smirnov test for goodness of fit. Journal of the American statistical Association, 1951. 4
[4] James Bergstra and Yoshua Bengio. Random search for
hyper-parameter optimization. JMLR, 2012. 2, 4, 6
[5] Hieu Pham, Melody Y Guan, Barret Zoph, Quoc V Le, and
Jeff Dean. Efficient neural architecture search via parameter
sharing. In ICML, 2018. 2, 6, 7
[6] Hanxiao Liu, Karen Simonyan, and Yiming Yang. Darts:
Differentiable architecture search. In ICLR, 2019. 2, 7, 8